Android Studio提交代码到SVN
本文共 2910 字,大约阅读时间需要 9 分钟。
目的:1、将AndroidStudio中的Android项目提交给svn;2、从svn下载已存储的android项目。
准备条件:1、svn客户端和服务端;2、创建一个android项目
步骤:
1、安装svn客户端
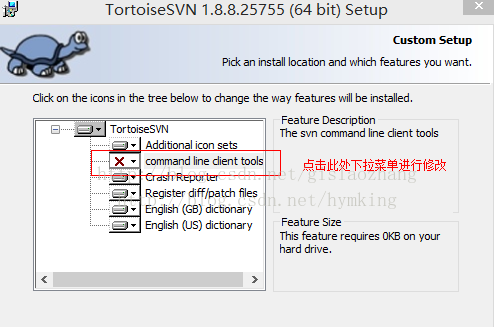
当出现这个页面时,在下拉框里选择第一个;
安装完后找到它的安装路径并找到bin目录,然后将整个路径复制下来,例如D:\Java\TortoiseSVN\bin。

接着进行AndroidStudio的相关配置,点击File–>Settings

然后会打开设置页面,找到Version Control —>Subversion;
在右侧的页面找到General选项卡,在User command line client:栏中补全svn的地址,记住最后一定要加上svn.exe

这个时候就将svn配置好了。
2、安装svn服务端
(1.为什么要用VisualSVN Server,而不用Subversion? 回答:因为如果直接使用Subversion,那么在Windows 系统上,要想让它随系统启动,就要封装SVN Server为windws service,还要通过修改配置文件来控制用户权限,另外如果要想以Web方式【http协议】访问,一般还要安装配置Apache,如果是新手,岂不是很头痛?而VisualSVN Serve集成了Subversion和Apache,省去了以上所有的麻烦。安装的时候SVN Server已经封装为windws service,Apache服务器的配置也只是在图像界面上,指定认证方式、访问端口等简单操作;另外,用户权限的管理也是通过图像界面来配置。 2.为什么不用TFS? 回答:因为我们一开始就是用Subversion和TortioseSVN,所以就没有更换其他的软件。至于TFS至今没有用过,其实,我只是看了一些的文章而已,对它也不了解。 3.VisualSVN Server是免费的吗? 回答:是的,VisualSVN Server是免费的,而VisualSVN是收费的。VisualSVN是SVN的客户端,和Visual Studio集成在一起, VisualSvn Server是SVN的服务器端,包括Subversion、Apache和用户及权限管理,优点在上面已经说过了。)
安装好VisualSVN Server后,运行VisualSVN Server Manger,下面是启动界面:

可以创建新的代码库以及用户(开发人员、测试人员、项目经理)和小组,设置用户不同权限。

3、在android studio中创建一个android项目
(略)
4、将android项目提交给svn
首先,从svn服务端得到上传代码的代码库地址(在创建的代码库上鼠标右键——>'Copy URL to clipboard'),得到代码库地址,
例如:https://PC-20160928OQEQ/svn/DataTool20170817/
其次,在AndroidStudio中创建忽略文件 (在上传之前一定要忽略一些文件,否则在上传的时候,AndroidStudio检测到了,会自动断掉上传。) 创建忽略文件的步骤为File–>Settings找到Version Control —> Ignored Files.具体要忽略的可以大体的分为以下几种。 (1)文件:local.properties;这个文件中包含了sdk的存储路径,因为每个人的存储路径都有可能会不太相同,所以还是建议忽略了比较好。当然不忽略也没错。 (2)文件夹: 以点开头的所有文件夹都要忽略,其中包括:.gradle和.idea; 然后就是所有的build文件夹, 注意是文件夹不是文件 ,如果将build的文件忽略了也会自动停止上传。包括:app目录下的build和总目录下的build。
(3)所有文件:*.iml这个没有什么好解释的

忽略文件做好了,就是要将代码分享出去了。 点击VCS——> Import into Version Control ——> Share Project(Subversion);

然后会弹出这样一个界面,这个时候你从服务器上获取到的地址就用上了,上面显示的就是已经添加好的,如果你没有地址可以点击" + "进行添加,添加完后双击网址,然后输入用户名和密码,就是服务端的用户名和密码(用户账号和密码)。点击右下角的记住就行,我这里已经记住密码了,没有办法再进行演示了。
添加完地址后选择好目录点击Share就好了。我一般选择第二个。

然后点完以后就是等待了。等进度条走完后一般来说就会变颜色。注意这个时候仅仅只是分享了,并没有实际上传。(如果分享的项目小的话,进度条走的会非常快,如果大的话就会非常慢,其实也不是很慢,第一次慢以后就好了)
接着,将代码提交到svn
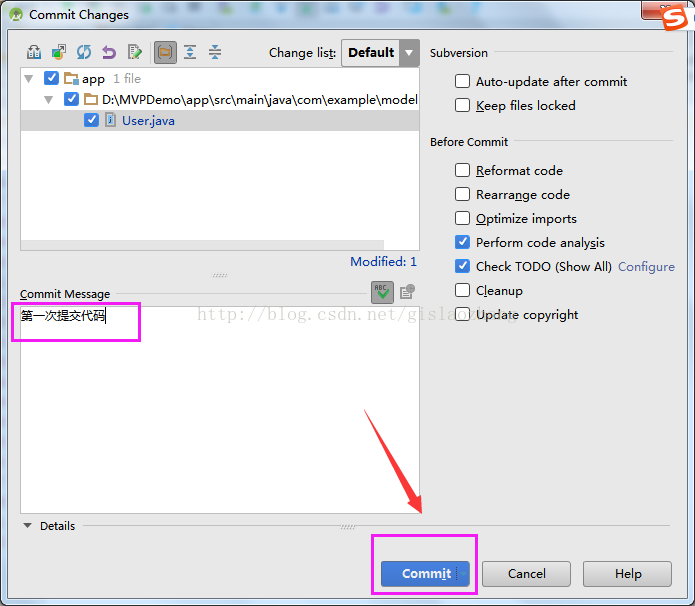
一般将代码分享到svn以后状态栏上就会出现这样的两个图标,蓝色的是同步svn的代码,就是从svn上下载;绿色的就是提交到svn,就是上传。这个时候点击上传的按钮就会出来一个下面这个界面。

然后点击commit就行了。 如果再弹出其他的消息栏还是点击Commit就ok了,这个时候代码就上传完了,等进度条走完了那么文件的颜色还是会变会原来的样子。
5、从svn下载android项目
首先打开欢迎界面,可以从将当前的工程关闭了,就可以找到这个欢迎界面了(File ——> Close Project )。

然后从这个页面选好要下载的项目,点击Checkout就行了,然后选择好下载目录点击ok;
在之后的弹出页面中,从Destination中选择好了要下载的项目,然后就点击ok。



在弹出的界面选择format,如果有1.8最好使用1.8(这个应该是svn的版本号)

点击ok后就会开始下载了,这个时候回弹出一个是否打开项目的选项,点击yes就行了。
弹出这个页面,直接无脑OK。
(这个时候如果卡在这个界面,原因有两点第一:项目正在构建,等待会就好了,一般不会超过半个小时。第二:sdk版本不一致,如果这个时候能够翻墙最好,如果不能翻墙,那还是拷一份一样的sdk吧。)

至此上传下载都已讲完。
---------------------------------------------------------------------------------------------------------------------------------
参考资料
http://blog.csdn.net/lincyang/article/details/5658274 //VISUAL SVN安装及客户端使用
http://blog.csdn.net/l_zhp/article/details/51030715 //Android Studio提交代码到SVN
http://www.cnblogs.com/ttzhang/archive/2008/11/03/1325102.html
你可能感兴趣的文章
Nginx 中解决跨域问题
查看>>
nginx 代理解决跨域
查看>>
Nginx 做负载均衡的几种轮询策略分析
查看>>
Nginx 入门,一篇搞定!
查看>>
Nginx 利用代理转发请求示例
查看>>
Nginx 动静分离与负载均衡的实现
查看>>
Nginx 反向代理 MinIO 及 ruoyi-vue-pro 配置 MinIO 详解
查看>>
nginx 反向代理 转发请求时,有时好有时没反应,产生原因及解决
查看>>
Nginx 反向代理+负载均衡
查看>>
Nginx 反向代理解决跨域问题
查看>>
Nginx 反向代理配置去除前缀
查看>>
nginx 后端获取真实ip
查看>>
Nginx 多端口配置和访问异常问题的排查与优化
查看>>
Nginx 如何代理转发传递真实 ip 地址?
查看>>
Nginx 学习总结(16)—— 动静分离、压缩、缓存、黑白名单、性能等内容温习
查看>>
Nginx 学习总结(17)—— 8 个免费开源 Nginx 管理系统,轻松管理 Nginx 站点配置
查看>>
Nginx 学习(一):Nginx 下载和启动
查看>>
nginx 常用指令配置总结
查看>>
Nginx 常用配置清单
查看>>
nginx 常用配置记录
查看>>